Toán 7-Giải đề thi học kỳ II/2020 - Kiến thức là vô hạn

Bài 1 a.

Dấu hiệu ở đây là điểm kiểm tra môn toán của lớp 7A.

Lớp có 3×10 = 30hs

Bảng tần số:

Điểm	2	3	4	5	6	7	8	9	10
tần số	3	5	4	4	4	3	4	2	1

Điểm trung bình cộng môn toán là

\frac{2 x 3 + 3 x 5 + (4 + 5 + 6 + 8) x 4 + 7 x 3 + 9 x 2 + 10 x 1}{30} = 5, 4

Bài 2. Cho đơn thức

A = (\frac{- 4}{3} x^{4} y) . (\frac{1}{2} x^{2} y) a . T h u g ọ n A = \frac{- 2}{3} x^{6} y^{2} b . G i á t r ị đ ơ n t h ứ c t ạ i x = - 1 v à y = 2 A = \frac{- 2}{3} . {(- 1)}^{6} . 2^{2} = - \frac{8}{3}

Cho 2 đa thức

A (x) = - 2 x + 2 x^{3} - 5 + x^{2} v à B (x) = - 3 x + x^{2} + 1 + x^{3}

a. Sắp xếp đa thức theo lũy thừa giảm dần của biến

A (x) = 2 x^{3} + x^{2} - 2 x - 5 B (x) = x^{3} + x^{2} - 3 x + 1

b . T í n h P (x) = A (x) + B (x) P (x) = 3 x^{3} + 2 x^{2} - 5 x - 4 Q (x) = A (x) - B (x) Q (x) = x^{3} + x - 6

c. Tính P(1), Q(-1)

P (1) = 3 . 1^{3} + 2 . 1^{2} - 5.1 - 4 = - 4 Q (- 1) = {(- 1)}^{3} + (- 1) - 6 = - 8

Hình học:

a . C M ∆ A H B = ∆ A H C X é t 2 t a m g i á c v u ô n g ∆ A H B v à ∆ A H C v u ô n g t ạ i H c ó : A B = A C (g t) \overset{\land}{B} = \overset{\land}{C} (g t) v ậ y ∆ A H B = ∆ A H C (c ạ n h h u y ề n - g ó c n h ọ n)

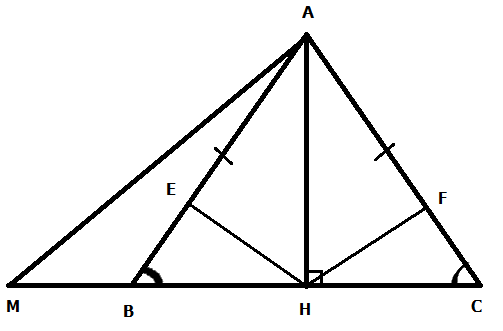
b. CM H là trung điểm BC. Tính AH.

Từ CM câu a. ta suy được HB=HC=BC/2 (cạnh tương ứng)

suy ra H là trung điểm BC

Tính AH. Theo pitago trong

∆ v u ô n g A H B v u ô n g t ạ i H c ó A C^{2} = H A^{2} + H C^{2} \Rightarrow H A^{2} = A C^{2} - H C^{2} \Rightarrow H A^{2} = 10^{2} - 6^{2} = 100 - 36 = 64 \Rightarrow H A = 8 c m

c . C M ∆ B H E = ∆ C H F X é t 2 t a m g i á c v u ô n g ∆ B H E v à ∆ C H F c ó : B H = H C (c m t) \overset{\land}{B} = \overset{\land}{C} (g t) v ậ y ∆ B H E = ∆ C H F (c ạ n h h u y ề n - g ó c n h ọ n)

d. CM: AM>AC

Xét tam giác vuông AMH có:

AM>AB (vì MH>BH)

mà AC=AB(gt)

=> AM>AC (đpcm)